Leduc Holdem

Training CFR on Leduc Hold'em. To show how we can use step and stepback to traverse the game tree, we provide an example of solving Leduc Hold'em with CFR: First, we install RLcard and Tensorflow. To use Tensorflow implementation of the example algorithms, we recommend installing the supported verison of Tensorflow with rlcardtensorflow. Leduc Hold’em is a two player poker game. The deck used in Leduc Hold’em contains six cards, two jacks, two queens and two kings, and is shuffled prior to playing a hand. At the beginning of a hand, each player pays a one chip ante to the pot and receives one private card. Solving Leduc Hold’em Counterfactual Regret Minimization From aerospace guidance to COVID-19: Tutorial for the application of the Kalman filter to track COVID-19 A Reinforcement Learning Algorithm for Recycling Plants.

1. Leduc Hold'em
2. Leduc Hold'em Strategy
3. Leduc Hold'em Rules

RLCard is a toolkit for Reinforcement Learning (RL) in card games. It supports multiple card environments with easy-to-use interfaces. The goal of RLCard is to bridge reinforcement learning and imperfect information games. RLCard is developed by DATA Lab at Texas A&M University and community contributors.

• Official Website: http://www.rlcard.org
• Tutorial in Jupyter Notebook: https://github.com/datamllab/rlcard-tutorial
• Paper: https://arxiv.org/abs/1910.04376
• GUI: RLCard-Showdown
• Resources: Awesome-Game-AI

News:

• We have released RLCard-Showdown, GUI demo for RLCard. Please check out here!
• Jupyter Notebook tutorial available! We add some examples in R to call Python interfaces of RLCard with reticulate. See here
• Thanks for the contribution of @Clarit7 for supporting different number of players in Blackjack. We call for contributions for gradually making the games more configurable. See here for more details.
• Thanks for the contribution of @Clarit7 for the Blackjack and Limit Hold'em human interface.
• Now RLCard supports environment local seeding and multiprocessing. Thanks for the testing scripts provided by @weepingwillowben.
• Human interface of NoLimit Holdem available. The action space of NoLimit Holdem has been abstracted. Thanks for the contribution of @AdrianP-.
• New game Gin Rummy and human GUI available. Thanks for the contribution of @billh0420.
• PyTorch implementation available. Thanks for the contribution of @mjudell.

Cite this work

If you find this repo useful, you may cite:

Installation

Make sure that you have Python 3.5+ and pip installed. We recommend installing the latest version of rlcard with pip:

Alternatively, you can install the latest stable version with:

The default installation will only include the card environments. To use Tensorflow implementation of the example algorithms, install the supported verison of Tensorflow with:

To try PyTorch implementations, please run:

If you meet any problems when installing PyTorch with the command above, you may follow the instructions on PyTorch official website to manually install PyTorch.

Leduc Hold'em

We also provide conda installation method:

Conda installation only provides the card environments, you need to manually install Tensorflow or Pytorch on your demands.

Examples

Please refer to examples/. A short example is as below.

We also recommend the following toy examples in Python.

R examples can be found here.

Demo

Run examples/leduc_holdem_human.py to play with the pre-trained Leduc Hold'em model. Leduc Hold'em is a simplified version of Texas Hold'em. Rules can be found here.

We also provide a GUI for easy debugging. Please check here. Some demos:

Available Environments

We provide a complexity estimation for the games on several aspects. InfoSet Number: the number of information sets; InfoSet Size: the average number of states in a single information set; Action Size: the size of the action space. Name: the name that should be passed to rlcard.make to create the game environment. We also provide the link to the documentation and the random example.

Game	InfoSet Number	InfoSet Size	Action Size	Name	Usage
Blackjack (wiki, baike)	10^3	10^1	10^0	blackjack	doc, example
Leduc Hold’em (paper)	10^2	10^2	10^0	leduc-holdem	doc, example
Limit Texas Hold'em (wiki, baike)	10^14	10^3	10^0	limit-holdem	doc, example
Dou Dizhu (wiki, baike)	10^53 ~ 10^83	10^23	10^4	doudizhu	doc, example
Simple Dou Dizhu (wiki, baike)	-	-	-	simple-doudizhu	doc, example
Mahjong (wiki, baike)	10^121	10^48	10^2	mahjong	doc, example
No-limit Texas Hold'em (wiki, baike)	10^162	10^3	10^4	no-limit-holdem	doc, example
UNO (wiki, baike)	10^163	10^10	10^1	uno	doc, example
Gin Rummy (wiki, baike)	10^52	-	-	gin-rummy	doc, example

API Cheat Sheet

How to create an environment

You can use the the following interface to make an environment. You may optionally specify some configurations with a dictionary.

• env = rlcard.make(env_id, config={}): Make an environment. env_id is a string of a environment; config is a dictionary that specifies some environment configurations, which are as follows.
  • seed: Default None. Set a environment local random seed for reproducing the results.
  • env_num: Default 1. It specifies how many environments running in parallel. If the number is larger than 1, then the tasks will be assigned to multiple processes for acceleration.
  • allow_step_back: Defualt False. True if allowing step_back function to traverse backward in the tree.
  • allow_raw_data: Default False. True if allowing raw data in the state.
  • single_agent_mode: Default False. True if using single agent mode, i.e., Gym style interface with other players as pretrained/rule models.
  • active_player: Defualt 0. If single_agent_mode is True, active_player will specify operating on which player in single agent mode.
  • record_action: Default False. If True, a field of action_record will be in the state to record the historical actions. This may be used for human-agent play.
  • Game specific configurations: These fields start with game_. Currently, we only support game_player_num in Blackjack.

Once the environemnt is made, we can access some information of the game.

• env.action_num: The number of actions.
• env.player_num: The number of players.
• env.state_space: Ther state space of the observations.
• env.timestep: The number of timesteps stepped by the environment.

What is state in RLCard

State is a Python dictionary. It will always have observation state['obs'] and legal actions state['legal_actions']. If allow_raw_data is True, state will also have raw observation state['raw_obs'] and raw legal actions state['raw_legal_actions'].

Basic interfaces

The following interfaces provide a basic usage. It is easy to use but it has assumtions on the agent. The agent must follow agent template.

• env.set_agents(agents): agents is a list of Agent object. The length of the list should be equal to the number of the players in the game.
• env.run(is_training=False): Run a complete game and return trajectories and payoffs. The function can be used after the set_agents is called. If is_training is True, it will use step function in the agent to play the game. If is_training is False, eval_step will be called instead.

Advanced interfaces

For advanced usage, the following interfaces allow flexible operations on the game tree. These interfaces do not make any assumtions on the agent.

• env.reset(): Initialize a game. Return the state and the first player ID.
• env.step(action, raw_action=False): Take one step in the environment. action can be raw action or integer; raw_action should be True if the action is raw action (string).
• env.step_back(): Available only when allow_step_back is True. Take one step backward. This can be used for algorithms that operate on the game tree, such as CFR.
• env.is_over(): Return True if the current game is over. Otherewise, return False.
• env.get_player_id(): Return the Player ID of the current player.
• env.get_state(player_id): Return the state that corresponds to player_id.
• env.get_payoffs(): In the end of the game, return a list of payoffs for all the players.
• env.get_perfect_information(): (Currently only support some of the games) Obtain the perfect information at the current state.

Leduc Hold'em Strategy

Running with multiple processes

RLCard now supports acceleration with multiple processes. Simply change env_num when making the environment to indicate how many processes would be used. Currenly we only support run() function with multiple processes. An example is DQN on blackjack

Library Structure

The purposes of the main modules are listed as below:

• /examples: Examples of using RLCard.
• /docs: Documentation of RLCard.
• /tests: Testing scripts for RLCard.
• /rlcard/agents: Reinforcement learning algorithms and human agents.
• /rlcard/envs: Environment wrappers (state representation, action encoding etc.)
• /rlcard/games: Various game engines.
• /rlcard/models: Model zoo including pre-trained models and rule models.

Evaluation

The perfomance is measured by winning rates through tournaments. Example outputs are as follows:

For your information, there is a nice online evaluation platform pokerwars that could be connected with RLCard with some modifications.

More Documents

For more documentation, please refer to the Documents for general introductions. API documents are available at our website.

Contributing

Contribution to this project is greatly appreciated! Please create an issue for feedbacks/bugs. If you want to contribute codes, please refer to Contributing Guide.

Acknowledgements

We would like to thank JJ World Network Technology Co.,LTD for the generous support and all the contributions from the community contributors.

by Nick Christenson

This article originally appeared in the February 2010 issue of TwoPlusTwo Magazine.

Preliminaries

Last time around I discussed a paper on optimal strategies for poker from the University of Alberta's Computer Poker Research Group (CPRG). This month I examine a paperfrom the same group on the issue of opponent modeling. It is titled,'Bayes'Bluff: Opponent Modeling in Poker'. It was presented at the 21st Conference on Uncertainty in Artificial Intelligence (UAI)in 2005.

There are two ways to approach creating a winning poker algorithm,and both are important in understanding the game. The first is tryingto play the game optimally, that is, trying to 'solve' the game. However,as was discussed in the last article in this series, by no means doesplaying optimally guarantee that one will win the most money. It justguarantees you won't lose (or, in the case of negative-sum games, youwill do no worse than lose your share of the rake.) In order to maximizeprofits against opponents that don't play optimally, one must understandtheir strategy and then compute a response against it that maximizesprofit. The first step in doing this, understanding opponents' strategy, is called 'opponent modeling'.

Bayesian Poker

One of the ways to model an opponents strategy is using a mathematicaltechnique called Bayesian statistics. This is based around Bayes theorem.It's easy to misunderstand what Bayes theorem actually says, so I'll tryto explain it as simply as I can.

Suppose there are two events, A and B, and they influence each other.If we find out that B has occurred, then the probability that A willalso occur depends not only on the probabilistic relationship betweenA and B, but also on the probability that A will occur independentlyof the information that B has occurred.

Here's an example. Suppose we know that sometimes after it rains, italso snows. Suppose we go outside and see that it's snowing? Whatdoes that tell us about whether it was raining earlier? If we knowthe odds of it snowing after it rains, that's only part of the picture.We also need to know the odds that it could just snow without raining.If we have both of these pieces of information, then using Bayesianstatistics we can make a prediction about the likelihood that it wasraining earlier.

In the abstract case, if we don't know anything about whether or notB occurred, then in a vacuum we may still make a prediction about theprobability that A will occur. In the example this corresponds to the probability that it might have just rained today. This probability distribution is called a 'prior', as it's what we think the likelihood of some event is 'prior' to having any additional information that would influence our opinion.

If we know B, or whether or not it's snowing in the example, that can change our estimate of whether or not it might have been raining earlier. Thisnew probability distribution is called the 'posterior' (meaning 'after').Yes, statistics students make jokes about this. On rare occasion they'reeven funny. I bring this whole thing up because in the 'Opponent Modeling' paper I'm discussing, if you don't understand what 'prior' and 'posterior'mean you'll be completely lost.

Sometimes Bayes' theorem sounds like simple if/then conditional probabilities. It's more than that. This can be confusing. In any case, this technique can be used to model poker opponents. If we know what players show down and what percentage of the time they adopt variousbetting strategies, we can make some estimates about how they wouldplay various hands. From that make predictions about what hand ranges they might hold.

Introduction

The paper begins with the authors setting the stage for whatthey're going to demonstrate. Assuming our opponent plays sub-optimally, to maximize profit we must take two steps:

1. Figure out our opponent's strategies.
2. Determine a best response to their plays, including their mistakes.

Neither step is trivial, and both are discussed in this paper.

Several approaches to this problem are possible, and good solutions aredifficult. This difficulty has several causes. First, we won't everhave complete knowledge of our opponents' strategy. This is due both tothe fact that we'll never have enough information to fill in all the gaps, and it's unlikely that our opponent will continue to play the way they always have.

Poker

The second section of the paper is more routine for poker players thanit is for mathematicians or artificial intelligence researchers. Theauthors first define the characteristics of a generic hold 'em game: Each player is dealt one or more hole cards, there will be one or more board cards, there will be two or more rounds of betting, and between rounds of betting one or more additional board cards will be revealed. The authors are examining two-player limit Texas hold 'em, as has traditionallybeen the focus of the CPRG folks.

In addition to looking at Texas hold 'em, they also examining anabbreviated game, which they call 'Leduc hold 'em'. Leduc is a smalltown near Edmonton, near the home of the University of Alberta and the CPRG. This game is similar in purpose to Rhode Island hold 'em, which was explained in an earlier article. The naming is essentially the same joke. I guess the difference is that Canada doesn't have any truly small provinces.For research purposes, the nice thing about Leduc (or Rhode Island) hold 'em is that it has many of the same characteristics of Texas hold 'em, but is small enough that optimal strategies can be determined explicitly.

The authors then go on to discuss some of the difficulties in creatinggood poker playing algorithms, but I won't discuss those here becausewhat they have to say is quite accessible in the paper.

Leduc Hold'em Rules

Modeling the Opponent

When modeling the opponent, the authors assume their opponent's strategy is 'stationary', that is, it's not changing overtime. Of course, this is a bad assumption to make for poker players in general. It precludes dealing with players who learn over time,and it precludes adjusting effectively to players who change gears,but it's a good place to start. As an extension of this, they also assume hands are 'i.i.d.', which stands for 'independent and identically-distributed'. This means that in addition to nothaving the effects of one hand influence subsequent hands, the game is fair.

Before we can build a strategy for our opponent, we must come up witha representation for the data we'll store about each hand in somedatabase. The authors explain that for each sample hand they're usingto derive an opponent strategy they're storing hole card informationfor both players (when available), board cards, and the bet sequencefor each betting round.

The idea is that when we see a given hand being played, we can compareit to previous hands in our database, and come up with a Bayesianprobability distribution for the types of hands our opponent might have. This distribution is what is called the 'posterior'.

Responding to the Opponent

Having a distribution of what we think our opponent's possible handsmight be is only half the battle. Now we must compute a response tothis hand range. The authors consider several options:

Bayesian Best Response (BBR) - This is a direct computation of thehighest EV response given the expected distribution of all possible hole cards. The authors point out that solving this is equivalent to solving something called theExpectimax algorithm.The Expectimax algorithm is the solution to a game tree where we are pickingeach node on the tree such that we expect to maximize our expectation forthe game. It's sort of a multi-round generalization of the Minimaxalgorithm of elementary game theory. The problem with BBR is that it'svery difficult to compute, even if you have all the information you need.So, for a 'real' poker game, this isn't practical. The best we can dois find approximations for BBR.

Max a posteriori response (MAP response) - 'a posteriori' is Latin for'from the latter', meaning 'from effects to causes'. In this method what we do is determine the best possible result for our opponent given the strategy they're playing, and then just calculate what our best responseis to that strategy. For complex games this isn't trivial either, but it's much easier than computing a BBR solution.

Thompson's Response - Here we pick a strategy from our opponent's distribution of previous hands weighted by Bayes theorem and play a best response to that particular strategy. In some sense, with MAPwe find a counter-strategy to the worst-case scenario. With Thompson'swe find a counter-strategy to the most likely scenario.

Later in the paper the authors will compare each of these methods of determining a response to an opponent's play.

Priors

What we call the 'prior' is equivalent to what most poker players would call an opponent's hand database. Without a good prior we can't make goodguesses about how our opponent's actions correspond with previous play,and without this information we have no chance of calculating a profitable response.

A good prior should have several properties. It should capturethe strategy of our opponent. It should be set up to make it easy tocalculate our posterior. It's structure should make it easyto calculate good responses. Given all this, it should be as smallas possible. Obviously, some of these work in opposition to each other.Generating a good prior is not simple, and I'm not aware of a generalapproach to creating or improving a prior.

The authors explore different priors for the two different poker games. For Leduc hold 'em they use a Dirichlet distribution. This is a special kind of probability distribution that is appropriate for this situation. Unfortunately, I don't know how to explain the details of why they chose this particular distribution in simple terms, so you'll just have to trust the authors here. In any case, the game space is small enough so they can take a good sample of an opponent's play that spans many possible hand outcomes.

The second prior, which they use for the Texas hold 'em samples, is what they call an 'informed' prior. That is, a skilled player selectswhat he or she feels is a subset of hands that adequately represents someother player's strategy. They use these samples to create several parameters to define how an opponent plays. These are described in Table 1 of the paper. Many of these will seem quite familiar to anyone who has used opponent data gathering software designed for online poker. The parametersthe authors use include the following:

Results were averaged over 1000 trials for Leduc hold'em and 280trials for Texas hold'em. Each trial (what poker players wouldcall a session), consisted of 200 hands. For each trial1000 strategies were sampled from the prior and used foropponent modeling. Also in each trial, different Bayesian methods, BBR, MAP, and Thompson's, were used to come up with a responseto each strategy.

These algorithms also played against two otheropponents: 'Opti', which in Leduc hold 'em is the optimal strategy, anda 'bot called 'Frequentist', which is an adaptive opponent modeling program that corresponds to the 'Vexbot' opponent found in the commercially available Poki's Poker Academy software.

Results

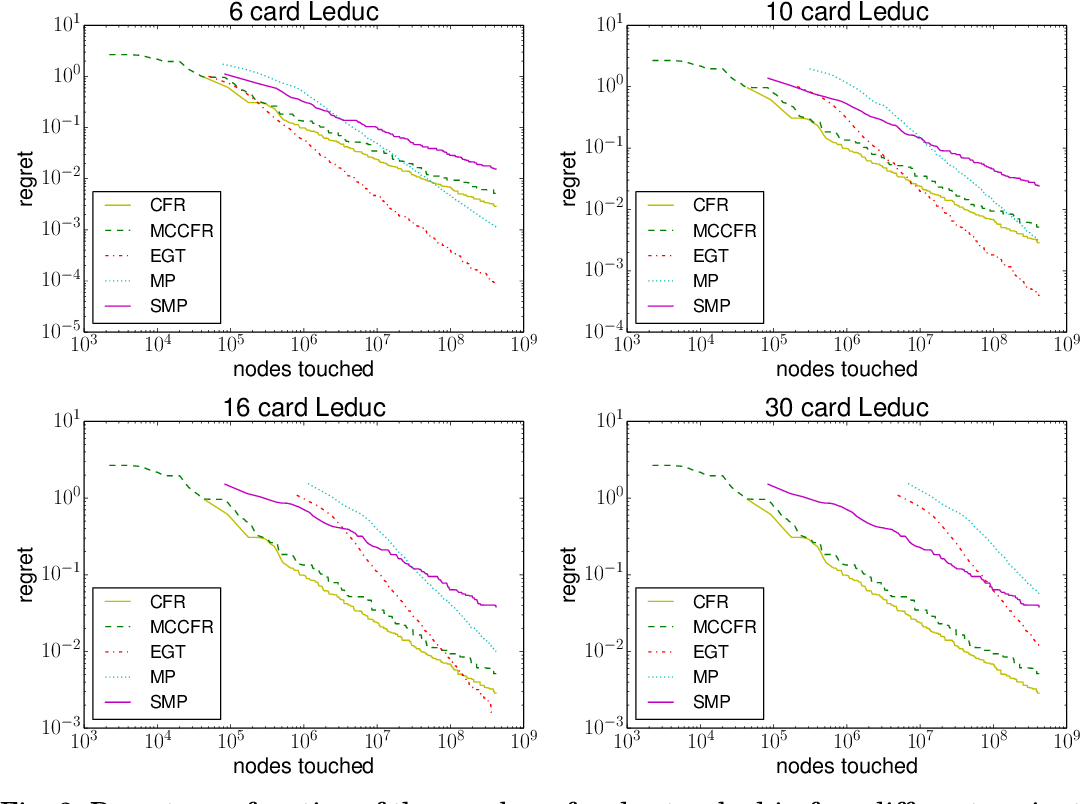
Leduc hold 'em:

The results of the various algorithms playing against the player are shown in Figure 2. Since for Leduchold'em we can explicitly compute the best possible response againstany strategy, that result is shown in the top line. Needless to say, none of the Bayesian strategies achieve this win rate. Of note, though,is that all of the Bayesian methods converge to similar results quitequickly. Moreover, all of them perform better than the Frequentistnon-Bayesian opponent modeling 'bot.

Note that all of these opponent modeling strategies produce a betterreturn than the Optimum strategy 'bot. By definition none of them played 'better' than Opti, but all of them played more exploitively. While the results are impressive, it would be easy to overstate their significance. Remember that our Bayesian models are playing against opponents employing stationary strategies from whom the prior was drawn. Clearly, though, these methods have some merit.

I want to point out that in paragraph 4 of section 7.1 the authors explain why they believe Frequentist didn't perform well. There is some good information here that I won't repeat, because I can't improve on what the authors said in that paragraph.

When the Bayesian models play against Opti, they all lose, which weexpect (actually, in the long run this has to be the case). Theperformance of each of the Bayesian models is again comparable. Also, once again the Bayesian 'bots do better than Frequentist.

The Bayesian models also win against Frequentist, although in thiscase Opti wins more. We also see some small divergence in long-termperformance of each of the Bayesian models with MAP and Thompson'soutperforming BBR. This is unexpected, and the authors discuss whythis might be the case in the last two paragraphs of section 7.1. To be honest, though, I find their justification a little unsatisfying.

Texas hold 'em:

For Texas hold'em we can't generate a Dirichlet prior, nor can we solve BBR for a game this complex. I expect that we also can't solve MAP, although the authors don't say so explicitly. In any case, thislimits the number of competitors to play against the the opponentwho generated the prior. These are Frequentist, Bayesian using the Thompson's response strategy, and Opti.

I don't know what Opti represents in this case; the authors don't say.Obviously, it can't represent a true optimal strategy as it does inthe Leduc hold 'em case. I presume it's the pseudo-optimal Opti algorithm as discussed in their previous paper, 'Approximating Game-Theoretic Optimal Strategies for Full-Scale Poker', which I discussed in aDecember '09 article.

In any case, both the Frequentist and the Bayesian opponents performedcomparably, with the Bayesian algorithm gaining a slight lead over Frequentist late in the contest. Both beat the non-exploitive Opti algorithm. The authors speculate that a 200 hand prior may nothave been enough for the Bayesian model to be able to assert a biggeradvantage over Frequentist.

Conclusions

This work shows that Bayesian methods of opponent modeling havepromise. Moreover, just a few hundred hands of data can provide usefulexploitive strategies, even for real poker games such as Texas hold 'em.

There are many areas of future work for this methodology that are likelyto be fruitful. One of these is research in coming up with better priors, both in terms of strategy and in terms of representing an opponent strategy in a minimal number of hands. Clearly, another avenue for exploration is to make these models more effective against opponentswho vary their strategies.